Voices of Biotech
Podcast: MilliporeSigma says education vital to creating unbreakable chain for sustainability
MilliporeSigma discusses the importance of people, education, and the benefits of embracing discomfort to bolster sustainability efforts.
When bioprocess liquids bearing suspended particles are filtered, retained particles can block and clog membrane filter pores. The pore size rating of a filter should be selected to retain objectionable particles by sieving, and the aptitude of its polymeric composition for adsorptive sequestration of those particulates also needs to be known. The quantity and nature of retained particles require accommodation if filtrative removal is to be considered successful. Too extensive a particle load will prematurely block a filter’s delivery of sufficient throughput to meet the filtration’s goal: obtaining enough drug product to provide an adequate monetary return. Drug processing thus represents a technoeconomic challenge.
In the first half of this two-part article (1), we examined fluid effects and operations (particle load; interactions of filtration area, differential pressure, and processing time; and operating conditions) as well as reviewed the results of several experiments involving latex particles and surfactants. Here we conclude by examining particulate effects and filter pore structure as well as further experimental findings.
PRODUCT FOCUS: BIOLOGICS
PROCESS FOCUS: DOWNSTREAM PROCESSING
WHO SHOULD READ: MANUFACTURING, ANALYTICAL, AND PROCESS DEVELOPMENT
KEYWORDS: MEMBRANE FILTRATION, MEMBRANE CHROMATOGRAPHY, FLOW RATE, ADSORPTIVE CAPTURE, PREFILTRATION
LEVEL: INTERMEDIATE

Dilute Particle Suspension Effects
The liquid suspensions Emory et al. used in their study of the effects of different surfactant types were more dilute than is customary (2). Examination of dilute particle suspensions is considerably significant. The investigations disclose insights not apparent from experimental results garnered using more concentrated suspensions. Dilute suspensions represent “worst-case” situations, those least encouraging to particle retention.
In more concentrated suspensions, it is conceivable that so many smaller particles may simultaneously arrive at a pore/fiber matrix as to give the appearance of its immediate blockage by a larger particle. This would more rapidly reduce the number of larger pores, over time lessening the opportunities for smaller particles to penetrate. It is a matter of the rate at which a sufficient mass of smaller particles reaches those larger pores to block them, as well as the number of individual smaller particles that escape capture during the period leading up to that blockage.
The time that larger pores are available for penetration by the separate smaller particles of dilute suspensions is foreshortened in concentrated dispositions, in which sudden pore blockages occur. Thus, the same total number of particles impacting a membrane over different durations can yield different throughputs. In essence, more dilute suspensions represent worst-case conditions because smaller individual particles are more likely to escape through still-unclogged larger pores.
Particle Size And Shape
As we see it, the stage on which a filtration act is played out consists of an effective filtration area (EFA) marked by a pore size or retention distribution that is confronted by a particle size distribution. A range of particle sizes is differentiated into two groups, each of which is defined by their size relative to the membrane pores. One portion comprises larger particles (too large to fit through any distributed pores or fiber matrices, whether large or small); the other portion consists of particles small enough to penetrate a membrane’s larger pores or fiber interstices, but not its smaller ones.
The pores or fiber interstices also comprise two size groups, only one of which covers a range of pore size ratings large enough to be passed through by the smaller particles. Depending on the relative proportion of smaller and larger particles present, and on the pore sizes they encounter (whether directed by the flow pattern or by chance), outcomes will be different for particle retention, the onset of filter plugging, and the quantity of throughput.
The definition of particle size is a bit too “neat” to apply absolutely to any particle shape except spheres directed toward circular pores. It begs an invariant sieving action based strictly on particle/pore sizes and ignores shape factors. Except for spheres, however, particle longitudinal and transverse axes may differ in size. In filtration, a particle’s dimensional axis coinciding with the pore functionally determines a particle’s size. Probability factors (e.g., a particle’s axial orientations) governed by liquid stream velocity, viscosity, and drag can cause more elongated shapes (needle-like) to pass through or lie athwart the pore openings. Thus, in a mixture of particles characterized generally as being too large to permeate a pore or fiber matrix interstice, some particular shapes may actually do so depending upon how their flow pattern is directed by either filtration conditions or by chance.
Equation 1: The Hagen–Poiseuille equation
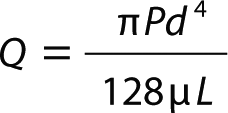
Q = volumetric flow rate of the test gas
P = applied differential pressure
d = pore diameter
µ = test gas viscosity
L = pore length through the membrane
It is not surprising that, in certain experimental trials, conclusions have been reached that some particles of a group-size seen as being “too large” to pass through a filter did, indeed, do so. This does not contradict the sieving mechanism, but rather more realistically describes size as defined by particle dimensions in an actual filtration. It might be simpler to refer to these particles as being “intermediate” in size. We are obliged, however, to describe such particles as they are referred to in the literature we’re quoting: namely as “larger particles.” That implies that they are too large to pass through a filter’s smaller pores, but that when properly aligned they can permeate a larger pore — bearing in mind, though, that pore size labels are generally descriptive and actual pore structures are typically larger than labeled. Keep this in mind during the following discussion.
Particle shape is not easily explained. Angular shapes (e.g., crushed stones), as seen while they rest heavy-side down under a microscope, can be expressed by a projected area. The diameter of a circle of equal area may be used to characterize such a particle, but the arbitrary nature of this designation is self-apparent. Nevertheless, it is the frame of reference underlying certain particle counters. Others may use the projected area or volume of a tumbling particle rather than its diameter. Both methods require development of correctional factors, which is not an easy undertaking. Characterizing particle size distributions is even more complex. To determine a filter’s efficiency in arresting particles of given size, the size distributions in both feed stream and filtrate must be known. But such information is usually unavailable.
The Structure of Filter Pores
The architecture of filter pores is little understood. Yet our comprehension of particle retentions requires some mental depiction of their sizes and shapes along with those of the particles they remove from fluids. The pores are not columnar in shape, though they are most often thought to be. Flow through pores and fibrous interstices is known to be tortuous to a degree determined by the concentration of the casting solution whereby a membrane is prepared. It attests to the competence of pharmaceutical processors that their drug purification methods are successful despite so much yet to be learned.
Macroscopically, a filter membrane looks like a polymeric froth reticulated and irregular in its cage-like morphology, similar to a sponge. Within such a structure, fluid flows in all directions. Under the impetus of differential pressure, individual openings within the polymeric or fiber matrix compose a pathway of least resistance to fluid flow. As Johnston (3) sees them, unlike the columnar pores of track-etched membranes, the pores of casting-process membranes are not integral passageways. Should arrested particles block parts of the chain of spaces, a fluid (differential pressure directed ad hoc) would use available next-best adjacent spaces to continue its flow.
The very few specific descriptions of “pores” show them as clusters of mixed, different-sized, polygonal-shaped cells connected by open walls that are also, therefore, of mixed sizes. Particles pass through the open walls leading from one hollow cell or chamber to another. “Pore size” is thus defined by the most open yet adequately size-restrictive dimensions of a successive chain of polygonal apertures that come to constitute a “traditional filter pore.” This is the view of Williams and Meltzer (4).
The most descriptive depiction of filter pores is provided by Zeman and Zydney (5), who see them as passageways consisting of an intimate sequence of chambers (“nodes”) of whatever size. Each of these polygons may be connected to many other nodes by way of a number of smaller apertures of different sizes. Those apertures are narrower spaces (“throats”), which are the restrictive pores (in relation to size, not flow) that connect the larger cells or nodes. Those constricted areas exercise the size discriminating mechanism of particle removal, so they are the “pores.”
Unlike filter membranes, prefilter materials do not have pores but rather interstices: openings within a random fiber matrix. As with pore structures, flow through the fiber matrix is tortuous rather than channeled. Any retentivity descriptions here depict porous membrane and fibrous interstice structures; for this reason it is important to consider both types of structures.
Experimental Findings And Conclusions
Experimentations of Lee et al (6) involved latex concentrations of 108 − 1010 per liter of each particle size (0.91 µm, 0.84 µm, 0.74 µm, 0.64 µm, and 0.45 µm) disposed in aqueous suspensions containing 0.1% of Triton X-100 surfactant at a pH of 7.1. Each individual suspension was used to exert a continuous challenge against a 0.45 µm-rated hydrophylized polyvinyllidene fluoride (PVDF) membrane. Zeman’s analysis of their experimental data (5) is of particular interest.
The log removal values (LRVs) obtained depended on particle loadings. Zeman refers to them as the “number of pore volumes of removed particles” (NPV). His analysis indicates that LRV levels decreased fourfold over the test’s duration. Plots comparing LRV and NPV showed five different traces for the five different latex bead diameters. The LRVs showed a strong dependence on particle loading. Interestingly, in more typical conditions (without surfactant) the five particle sizes would not differentiate, which in itself is an index of the experimental detail that comes from working with dilute suspensions. According to Zeman, filter blockage occurred from incipient cake formation when only 1% of the membrane pore volume was filled (NPV = 0.01). For the larger particles, a greater degree of filter cake build-up that ensued caused the falling LRV to undergo an increase at higher NPVs.
The more numerous the particles and the larger their size, the more rapidly was a filter’s porosity blocked to particle passage. The more rapid that blockage, the more restricted was a filter’s throughput. From their work with latex cross-linked polystyrene beads, Emory et al. (2) confirmed that “retention is strongly dependent on particle feed concentration.” And Zeman noted that filter LRVs decreased some fourfold during testing (5). That translates to a fourfold increase in particle passage and was attributed to blockage of smaller pores, likely to enhance smaller particle flows through larger pores with concomitant particle passage.
We agree with Zeman regarding the findings of Lee et al. These conclusions find support as well from other investigations involving dilute suspensions, which are more conventional in that they do not contain surfactant. Those have been analyzed and discussed by Meltzer and Jornitz (7), whose findings importantly influence the efficiencies of final filters and should be used in designing final-filter arrangements.
In the context of surfactant being present, Zeman based his analysis of “latex particle polydispersity” on finding that the presence of many larger particles reduced the passage of smaller particles. However, with more smaller particles, more of the “larger” particles passed through the filter. Zeman stated two propositions: “The breakthrough of the smaller particles is retarded by the presence of larger particles,” and “The passage of ‘larger’ particles occurs more rapidly when smaller particles are present in the stream.”
During filtration, a fluid is simultaneously directed to/through both smaller and larger pores. According to the mean flow-pore concept, a small number of larger pores carries one half the filter’s entire flow while the remaining pores carry the other half (8). A far greater number of pores smaller than the mean flow pore are needed to balance the influence of the hydrodynamic preference for larger pores. In line with the Hagen–Poiseuille equation (Equation
1), a greater proportion of smaller pores operating on the order of their radii to the fourth power will balance the larger pores’ greater flows.
With regard to particle retention, both larger and smaller particles would block small pores. Larger particles would similarly block larger pores. But smaller particles could permeate the larger pores. Blockage of the smaller pores will reduce their functional numbers, shifting the pore size distribution in the direction of the larger pores. That will increase the likelihood of smaller particle (organism) penetration in reverse proportion to the number of smaller pores still available. However, to the extent that the proportion of larger particles dominates, their encounters with larger pores will exceed those of the smaller particles, which speeds closure of those larger pores. Nevertheless, until pore closure is complete, small-particle passage can take place. The trend continues until all larger pores are effectively blocked as indicated by the rate of flow diminution.
So the initial rate of particle passage reflects the relative quantities of smaller and larger particles (and the numbers of smaller and larger pores) subject to mean flow-pore influences. As smaller pores become increasingly blocked (whether by larger or smaller particles), the rate of smaller particle permeation in proportion to the number of larger pores will increase, even as the number of available larger pores decreases. However, the rate of particle passage progressively decreases as those larger pores are successively blocked. The more larger particles are present, the faster is the closure of pores through which smaller particles can pass — and the fewer overall filter penetrations. The earlier filtration is terminated, the lesser the amount of throughput. This is identical to Zeman’s observation that the breakthrough of smaller particles is retarded by the presence of larger particles. The more larger particles are present, the shorter is the time interval during which smaller particles may pass through yet-unblocked larger pores.
How latex beads of different diameters (e.g., 0.91 µm, 0.84 µm, 0.74 µm, 0.64 µm, and 0.45 µm) might penetrate a given filter — for example, a 0.45-µm rated membrane — would depend on the presence or absence of a surfactant and its unique molecular identity. Interestingly, in a typical situation (without surfactant), those five different lattices would not show differentiation because they would all be subject to adsorptive sequestration. When surfactant is present, the larger lattice units are less likely than smaller ones to pass through a filter because their passage is more liable to be restrained by sieve retention.
Zeman’s second proposition — that passage of larger particles (in size and shape) occurs more rapidly with smaller particles present — is also correct. Smaller particles block only the smaller filter pores. Without adsorptive arrest, they have no effect on the progressive clogging of larger pores leading eventually to their blocking. In effect, small particle competition for occupying the smaller pores (even if due only to their numbers) increases the frequency of larger particles coinciding with the larger pores. To the extent that “larger” particles are of shapes with dimensions suitably oriented within the flow stream to negotiate larger-pore passage, the presence of smaller particles enhances their filter penetration.
Dilute Suspensions Without Surfactant
As we see it, in normal filtrations without surfactants, fluid flows and the particles they convey are exactly as they are in the presence of surfactant. Larger particles will block the pores they encounter, and small particles will block smaller pores. The only difference is that particles small enough to enter pores need not necessarily pass through them; they may be restrained by intrapore adsorption. The latter would depend on the polymeric nature of a given filter and on such conditions as the suspending fluid’s velocity, viscosity, and temperature (the reciprocal of its viscosity). Over time, increased clogging of the larger pores will progressively improve a filter’s rate of particle retention.
That sequence of steps explains what resulted when Grant and Zahka (9) challenged 0.45-µm rated PVDF membranes with dilute suspensions of latex particles of different sizes. (The latex particles averaged 0.605 µm, 0.652 µm, and 0.662 µm in size, and particle concentrations were from 1.2 × 108 to 1.4 × 109 particles per liter.) The filter’s retention capability decreased progressively from the start of filtration because of small particles permeating larger pores. Both entities were initially present. As larger pores became blocked by larger particles (and the progressive clogging of smaller particles), the filter experienced a recovery of its particle removal efficiency. As the filter’s porosity continued to decrease, its efficiency increased progressively. Particles could pass as long as the larger pores remained sufficiently open to passage. A further application of this phenomenon is seen from earlier retention recoveries manifested by the larger particles in a particle size mix. Similar findings were made by Roberts et al (10), and by Roberts and Velazquez (11). Figure 1 is reprinted with permission from Roberts et al.
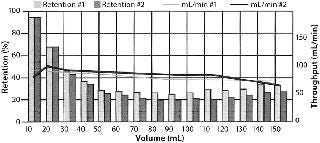
Figure 1: ()
Particle-Passage Amelioration
Based on the above reasoning, a predominance of smaller pores in a final filter (or interstices in a prefilter) would promote their early involvement in particle blockage. That scenario tends toward greater particle retention until the still-open smaller pores approach complete exhaustion. With fewer smaller pores initially, particle passage through the larger pores could begin more readily. Similarly, more smaller pores would slow the rate at which smaller particles would impact the larger pores. That would affect the probabilities of their passage. In actuality, the fixed number of smaller pores in a final filter relative to the number of smaller particles confronting it would determine the point and amount of particles that penetrate the larger pores.
The paramount consideration is that effluent from a (single) final filter consists of a dilute suspension of smaller particles from the original feed stream that has permeated that filter. However, if a prefilter were placed upstream of it, the inherent supply of smaller pores would reduce the frequency with which particles of any size could coincide with its larger pores. Thus, the rate of particle penetration would decrease.
Integration of the experimental findings of Lee et al. (6), their analysis by Zeman (5), the investigations by Grant and Zahka (9,12), and the independent confirmation by Roberts and Velaszquez (11) and Roberts et al. (10) seems to lead to the same conclusions regarding the interactions of different sized particles with different sized pores. Our synthesis of these investigative and analytical endeavors provides an understanding that the small particles of a dilute liquid suspension filtered through a membrane characterized by a larger number of smaller pores may produce a sterile product.
The role of a prefilter is to make possible those very circumstances. It limits the number of smaller particles that can encounter the larger pores of the final filter to penetrate it. It does so, in effect, by indirectly reducing the proportion of larger pores in a pore population. It actually diminishes the population of smaller particles that might successfully challenge the larger pores of the final filter. As the logic of Euclidian geometry has it, things equal to the same thing are equal to each other.
About the Author
Author Details
Corresponding author Russell E. Madsen is president of The Williamsburg Group, LLC, 18907 Lindenhouse Road, Gaithersburg, MD 20879-1817; 1-301-938-4266, fax 1-301-869-5016; [email protected]; www. thewilliamsburggroup.com. Theodore H. Meltzer is a consultant with capitola consultancy, and Maik W. Jornitz is group vice president for filtration and fermentation technologies at Sartorius-Stedim North America, Inc.
1.) Madsen, RE, TH Meltzer, and MW Jornitz. 2010. How Pore and Fibrous Interstice Structure Influence Filter Performance, Part 1: Fluid Effects and Operations. BioProcess Int 8:58-64.
2.) Emory, SF. 1993. The Effects of Surfactant Type and Latex-Particle Feed Concentration on Membrane Retention. Ultrapure Water 10:41-44.
3.) Johnston, PR 1992.Sterilization By FiltrationSecond Edition, Interpharm, Buffalo Grove:41-45.
4.) Williams, RE, and TH Meltzer. 1983. Membrane Structure: The Bubble Point and Particle Retention: A New Theory. Pharmaceut. Technol. 7:36-42.
5.) Zydney, AL Zeman, LJ and AL 1996.Chapter 4: Characterization of MF/UF MembranesMicrofiltration and Utrafiltration: Principles and Applications, Marcel Dekker, New York:180-291.
6.) Lee, JK, BYH Liu, and KL Rubow. 1993-a. Latex Sphere Retention By Microporous Membranes in Liquid Filtration. J. Inst. Environ. Sci. 36:26-36.
7.) Meltzer, TH, and MW Jornitz. 2006.Chapter 2. Pharmaceutical Filtration: The Management of Organism RetentionPDA, DHI Publishers, Bethesda.
8.) ASTM Standard F-316-03-2003 2003.Pore-Size Characteristics of Membrane Filters for Use with Aerospace Fluids, American Society for Testing and Materials, West Conshohocken.
9.) Grant, DC, and JG Zahka. 1990. Sieving Capture of Particles By Microporous Membrane Filters from Clean Liquids. Swiss Contam. Control Quart. 3:160-164.
10.) Roberts, KL, DJ Velazquez, and DM Stofer. 1990. Challenging the Membrane Filter Ratings. Semiconductor Int. 13:80-84.
11.) Roberts, KL, and DJ Velazquez. 1990. Characterizing the Rating and Performance of Membrane Filter for Liquid Applications Using Latex Spheres. Swiss Contam. Contr. Quart. 3:71-74.
12.) Zahka, JG, and DC Grant. 1991. Predicting the Performance Efficiency of Membrane Filters in Process Liquids Based on Their Pore-Size Ratings. Microcontamination:23-29.
You May Also Like