Voices of Biotech
Podcast: MilliporeSigma says education vital to creating unbreakable chain for sustainability
MilliporeSigma discusses the importance of people, education, and the benefits of embracing discomfort to bolster sustainability efforts.
March 1, 2012
Knowledge of kLa (the volumetric mass-transfer coefficient that describes the efficiency with which oxygen can be delivered to a bioreactor for a given set of operating conditions) is not new. Here I provide information for those who are unfamiliar with the measurement method and/or issues that must be considered when making these measurements. Advances in this area now make it advisable to run kLa measurements routinely in many bioprocesses.
The Importance of Measuring kLa
Before examining the process theory and tactical specifics of kLa determinations, it is essential to understand why kLa measurements are relevant and how they add value to bioprocesses. Dissolved oxygen (DO) is often the limiting substrate in fermentation and cell-culture systems. For bacteria and yeast cultures, the critical oxygen concentration is usually 10–50% of air saturation. Above that critical level, the oxygen concentration no longer limits growth. For optimum growth, it is therefore important to maintain DO levels above the critical value by sparging (bubbling gas through) the bioreactor with air or pure oxygen. Of course, to be effective, the mass transfer rate of oxygen to the liquid broth must equal or exceed the rate at which growing cells take up that oxygen.
PRODUCT FOCUS: ALL BIOPHARMACEUTICALS
PROCESS FOCUS: PRODUCTION
WHO SHOULD READ: PROCESS AND PRODUCT DEVELOPMENT
KEYWORDS: CELL CULTURE, BIOREACTOR, OXYGEN ANALYSIS,kla
LEVEL: INTRODUCTION

Measurements of kLa provide important information about a bioprocess or bioreactor. These determinations ensure that processing conditions are such that an adequate supply of oxygen is available for proliferation of cells. The kLa value can also be used to optimize control variables over the lifecycle of a bioprocess. Such optimization would be based on the oxygen demand at various points in the process and growth phase of the biological. Criteria for optimization may be product yield, power consumption, or processing time.
Applications
New equipment: Measurements of kLa are made when evaluating new reactor designs, new gas sparging equipment, and/or operating conditions. The goal in each case is to confirm that reactor conditions can support a system being processed at each point in its lifecycle.
Process Optimization: Measuring kLa is also critical during process optimization. In scale-up and manufacturing situations, fine-tuning bioreactor performance assumes greater significance. Measuring kLa is key to controlling oxygenation at the optimal rate (1).
Relevance to Single-Use Bioreactors: Determining kLa can be especially useful when companies make decisions about the role of single-use bioreactors in their overall manufacturing strategy. For those considering adopting single-use bioreactor technology and thinking about where and how to do so, kLa measurements can provide meaningful support for big investment decisions. The range of kLa values that a SUB can support, coupled with the operating conditions required to achieve that range, are fundamental in the selection of reactor equipment. A review of the process involved explains why.
Process Theory
The oxygen transfer rate (OTR) of a bioreactor is strongly influenced by the hydrodynamic conditions being used in the bioprocess it’s used in (Figure 1). These conditions are a function of energy dissipation that depends on the operating conditions, the physicochemical properties of a culture, the geometrical parameters of the bioreactor, and the presence of oxygen-consuming cells.
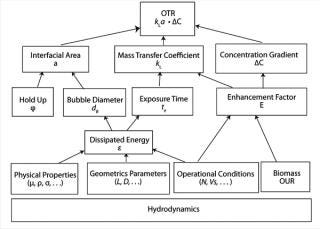
During cell culture, oxygen is transferred from a gas (typically a bubble or headspace) to a liquid, so it can ultimately be absorbed into a cell and consumed. In the simplest terms, this process can be described as the flux across a barrier layer expressed as the product of the driving force (mass imbalance) and mass transfer coefficient (kLa) in Equation 1 below:
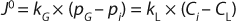
In that equation, J0 is the molar flux of oxygen (mol/m2s) through the gas–liquid interface, kG and kL are the local mass transfer coefficients, pG is the oxygen partial pressure in the gas phase, and CL is the dissolved oxygen concentration in the liquid. Index i refers to values at the gas–liquid interface.
Because interfacial concentrations are not directly measureable, it is common to consider a special case of Equation 1 that describes flux under or at equilibrium:

In Equation 2 above, p* is the oxygen pressure in equilibrium with the liquid phase, C* is the oxygen saturation in the bulk liquid, and KG and kL are the overall mass transfer coefficients. However, because the solubility of oxygen in water is very low and the vast majority of mass-transfer resistance is on the liquid side of the interface, the overall mass transfer coefficient can be assumed to be equal to the local coefficient (KL = kL). As a result, the oxygen mass transfer rate per unit of reactor volume (dCO2/dt) is obtained by multiplying the overall flux by the gas–liquid interfacial area per unit liquid volume using Equation 3
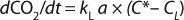
Quantification and Equations Used
The mass balance for the DO in the well-mixed liquid phase is described in Equation 4
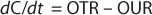
Here, dC/dt is the accumulation oxygen rate in the liquid phase, OTR represents the oxygen transfer rate from the gas to the liquid, and OUR is the oxygen uptake rate by the microorganisms. The last term can be expressed by the product qO2 × CX, with qO2 being the specific oxygen uptake rate of the microorganism used and CX is the biomass concentration.
In the absence of biomass or with nonrespiring cells, when biochemical reactions do not take place, OUR = 0. In this case, Equation 4 can be simplified as
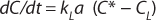
Because of the difficulty of measuring kL and a separately, the product kLa is treated as a single measureable variable: the volumetric mass transfer coefficient. Determination of kLa is achieved by recording the system response following a perturbation of the equilibrium oxygen concentration.
Integrating the expression of previous equation yields Equation 5
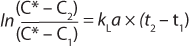
Here, Ci is the concentration of oxygen at time ti. For the case of a system perturbation that increases the DO concentration from an initial value of 0, this equation becomes
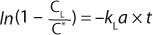
For the case of a perturbation that decreases the dissolved oxygen concentration, the equation becomes
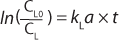
Factors Affecting kLa
Multiple Variables: As illustrated in Figure 1, kLa is influenced by many variables. Factors include everything from a bioreactor’s size and design to the sparging of gas, mixing, cell line, media type, temperature, pH, salt content, and antifoaming agents (2). Every time one of those factors changes, the dynamics of the bioprocess, including kLa, change as well. Given such broad vulnerability, it is not surprising that actual in-process kLa measurement has been limited. Scientists have relied to a large extent on the built-in functionality of the bioprocesser to maintain proper oxygen flow rate.
Speed: Because kLa measurements involve monitoring levels of DO following a system perturbation, the results can be influenced by the response time (or “speed”) of a sensor making those determinations. Sensors with response times (τr) on the order of the first-order time constant of the mass transfer (1/ kLa) require special treatment of their data to correct for the time lag in readings introduced by the oxygen sensor.
A general rule of thumb is that the sensor response time must be less than one tenth of the time constant for mass transfer for this effect to be negligible (3,4). When a sensors response time does not meet this requirement, the data must be treated with Equation 6
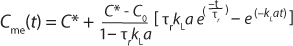
in which Cme(t) is the measured value of oxygen at time t. That equation cannot be linearized, so nonlinear fitting of observed response data is required to derive the value of kLa.
Changes in Reactor Vessel Size: The value of kLa is unique to both the size and configuration of a reactor vessel. Although some empirically derived expressions have been published for predicting kLa values in non-Newtonian fluids, there is no agreed upon set of equations that account for all of the variables that can affect the results. Accordingly, predicting kLa is not possible, and kLa studies need to be performed for bioreactors individually.
Measuring kLa
The value of kLa rate constants can be ascertained for virtually any reactor vessel, from a shaker flask to the most sophisticated single-use bioreactor. It is important to recognize that, as noted above, the sensitivity of kLa to many different factors also results in changes in the best way to measure it. Similarly, the differences in disposable bioreactor construction and operating methodology often indicate the need to modify the general instructions for kLa measurement. This is not necessarily difficult, but rather is simply a reflection of differences in bioreactors.
Benefits
Measuring kLa offers important benefits:
assurance that biological growth is not impeded by inadequate oxygen concentration
better ability to fine-tune oxygen concentration for optimal processing
prevention of wasted energy and cost associated with unnecessarily high oxygen concentrations
more informed equipment purchase decisions.
For companies engaged in bioprocessing, the ability to measure kLa easily and accurately represents a significant opportunity to improve the performance of their operations.
About the Author
Author Details
James Kane, PhD, is vice president of technology and product development at Polestar Technologies, Inc; 220 Reservoir Street #3, Needham Heights, MA, USA 02494; 1-781-449-2284; www.polestartech.com.
1.) Arrua, LA, BJ McCoy, and JM. Smith. 1990. Gas–Liquid Mass Trans
fer in Stirrer Tanks. AlChE J 36:1768-1772.
2.) Lydersen, BK, NA D’Elia, and KL Nelson.
3.) Weiland, P, and U. Onken. 1981. Fluid Dynamics and Mass Transfer in Airlift Fermentor with External Loop. Ger. Chem. Eng. 4:42-50.
4.) Godbole, SP. 1984. Hydrodynamics and Mass Transfer in Non-Newtonian Solutions in a Bubble Column. AlChE J. 30:213-220.
You May Also Like