Lessons in Bioreactor Scale-Up, Part 2: A Refresher on Fluid Flow and Mixing

Commercial-scale production of recombinant therapeutic proteins routinely involves suspension cultures of mammalian cells in bioreactors with up to 10,000 L capacity. With advances made over the past 30 years in cellular engineering, basal and feed media development, and bioprocess engineering, expression titers of ~10 g/L, viable-cell densities of >3 × 10⁷ cells/mL, and specific productivities of >20 pg/cell/day are now common. Such high cell densities (with the potential to go even higher) increase mixing and aeration demands and can subject cells to aggressive environments such that they experience high hydrodynamic stresses. This installment of my bioreactor scale-up series should refresh your knowledge of fluid flow, mixing, and mass transfer in bioreactors, including how the interplay of those parameters creates the environment that cells experience. That in turn influences their growth, metabolism, and protein production.

Fluid Flow in Bioreactors

Fluids — either liquids or gases — are substances that undergo continuous deformation when subjected to shear force. Shearing causes deformation, a change in the relative positions of fluid components. Such force must be applied to produce fluid flow (1). Scientists categorize fluids according to their density and viscosity as

• compressible (or incompressible) — whether their density changes (or not) in response to pressure, with gases generally being compressible and liquids being incompressible

• viscous (all fluids have a finite viscosity, which is responsible for “internal friction” during flow, otherwise expressed as a fluid’s resistance to motion)

• Newtonian or non-Newtonian, depending on whether they obey Newton’s law of viscosity.

Shear stress is calculated by dividing the shear force applied to a fluid by the cross-sectional area to which it is applied. Strictly speaking, shear stress is one of two types of fundamental hydrodynamic forces, the other being “normal stress.” Both are determined commonly as viscosity multiplied by the velocity gradient, with flow direction being perpendicular for shear stress and parallel for normal stress. Hence, a velocity gradient for shear stress is written as dU_x/dy and for normal stress as dU_x/dx, where U is the velocity of fluid and x and y represent the direction of the force/stress.

When fluid flows through a pipe or over a solid object, the velocity of that fluid changes depending on position. The fluid layer in contact with the wall of a pipe, for example, is assumed to have the same velocity as the wall or solid object (zero velocity). The next fluid layer inward has a bit higher velocity because of the overall fluid motion, the next layer inward has more, and so on. Within every fluid is a continuous exchange of particles among those layers, and that influences the velocity of their flow. Particles moving from a slow-moving layer to a faster layer will act to reduce its speed; those coming from a fast layer to a slower one will have an accelerating effect. Thus are shear stresses induced by fluid flow as a consequence of velocity differences.

Depending on fluid velocity, flow can be characterized as laminar or turbulent (Figure 1). When the overall fluid motion is slow, adjacent fluid layers move in an orderly (more or less parallel) motion called laminar flow. In a fast-moving fluid, particles and parcels of fluid frequently cross layers randomly and chaotically in a turbulent flow.

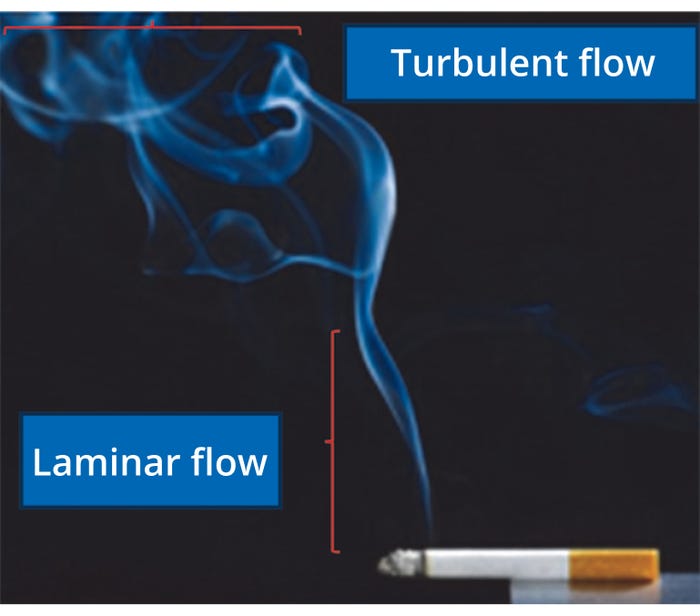
Figure 1: Familiar examples of laminar and turbulent flow.

Reynolds number (Re) is a dimensionless variable for characterizing fluid motion as laminar or turbulent. Equation 1 calculates Re for fluid flow in pipes with circular cross-section:

Re = DUρ/μ where D is the pipe diameter, U is fluid velocity, and ρ and μ are density and viscosity of the fluid, respectively.

Because the biopharmaceutical industry is concerned primarily with fluid flow in stirred-tank bioreactors, the relevant Reynolds number is defined by Equation 2:

Re_i = N_iD_i²ρ/μ where N_i is the stirrer speed, D_i is the impeller diameter, and ρ and μ are density and viscosity of the fluid, respectively.

Conceptually, the Reynolds number expresses the ratio of inertial to viscous forces. During laminar flow (low Reynolds number), viscous forces dominate, and fluid motion is slow. However, with increasing Reynolds numbers, inertial forces become more dominant, and flow transitions from laminar to turbulent — then becomes fully turbulent at sufficiently high Re values.

Pipe flow is laminar if Re < 2100. For Re values of 2000–4000, the flow is considered to be in a transition state from laminar to turbulent. It is fully turbulent once Re > 4000. In stirred tanks, the value of Re that marks the transition from laminar to turbulent flow depends on tank and impeller geometry.

Turbulent Flow in Bioreactors

Turbulent flow is the flow regime that cells encounter in bioreactors. Turbulence is essential for effective mixing (mass and heat transfer in fluids), so achieving turbulent-flow conditions in bioreactors is vital to culture success. As noted above, the Reynolds number indicates when turbulent flow is generated. As that number increases, inertial forces come to dominate viscous forces in the fluid, overcoming the tendency of viscous effects to dampen flow instability. Thus, turbulence can be regarded as a highly disordered fluid motion resulting from instabilities growing in an initially laminar flow field (1).

Turbulent flow is very complex by nature, so our understanding of it is far from complete. The flow has an overall direction, but superimposed on that are secondary chaotic movements of fluid particles causing flow deviations and generating vortices of varying shape, size, speed, and rotational direction. Those irregular secondary motions in turbulent flow have profound consequences for mixing efficiency, energy loss, and shear intensity. Turbulent flows develop spinning or swirling fluid structures called eddies, which can stretch, coalesce, and divide. Fluid velocity within an eddy undergoes great change in magnitude and direction within a relatively short distance and time.

Eddies of different sizes appear in turbulent flow. The size of the largest eddies is limited by the boundary of the flow system. Hence, the diameter of the largest eddies in a bioreactor is similar to (but somewhat smaller than) the diameter of the reactor vessel. Large eddies are unstable and give rise to smaller ones, which in turn produce even smaller eddies, and so on. In a stirred bioreactor, large eddies derive energy from the bulk flow generated by the impeller, so they contain most of the turbulent kinetic energy. The smallest eddies cannot sustain rotational motion and lose their energy as heat through the effects of viscosity and fluid friction. Maintaining turbulent flow thus requires continuous supply of energy to make up for what is lost as heat (1).

Dispersion is the process of breaking up the bulk flow into smaller and smaller eddies to facilitate rapid transfer of material throughout a tank. The degree of homogeneity possible as a result of dispersion is limited by the size of the smallest eddies that form. Assuming that isotropic turbulence is prevailing in a stirred tank and that flow is turbulent (N_Rei > 10⁴), the size of the smallest eddies is given approximately as the Kolmogorov scale of mixing (λ) or scale of turbulence, defined by Equation 3:

λ = (ν³/ε)^1/4

where λ is the characteristic length of the smallest eddies, ν is the kinematic viscosity of the fluid, and ε is the local rate of turbulent energy dissipation per unit mass of the fluid.

At a steady state, the average rate of turbulent energy dissipation throughout a bioreactor is equal to the power input by the impeller to the fluid within the tank. Hence, the greater the power input to the impeller, the smaller the eddies will be. Because λ depends on viscosity, smaller eddies are produced in low-viscosity media for a given power input. An energy input of 0.1 W/kg, which currently is considered to be high for animal-cell cultures, yields an estimate for the smallest eddy diameter λ of about 0.06 mm (60 μm). That represents the smallest scale of mixing achievable by dispersion under such conditions.

The characteristic length of the smallest eddies (λ) often is an indicator of the potential for cell damage caused by fluid shear. Experiments have shown that if biological entities (e.g., mammalian cells) are smaller than λ in a bioreactor, then shear damage to such entities will not occur. Minow et al. presented a comparative study of mixing and mass transfer in two different 1000‑L single-use bioreactors. The authors calculated the Kolmogorov length of the smallest eddies prevailing in each bioreactor type (2).

As Table 1 shows, the calculated values of λ for each bioreactor type were close to 80 μm — far larger than the 15-μm size of Chinese hamster ovary (CHO) cells used in the study. Similarly, Godoy-Silva et al. described CHO cells that could withstand power inputs ≤6000 W/kg (3). At power dissipation rates >300 W/kg, which is still much higher than the power densities in commercial cell-culture reactors, the only impact observed was in the glycosylation pattern of expressed proteins, but the cells were not affected (7). Even if such results are specific to the system studied, they still show that shear damaging has been overestimated in recent decades. Nienow arrived at the same conclusion in two different papers (4, 5). Hence, it is safe to say that eddies <10–20 μm (smaller than the typical mammalian cell size) possess very little turbulent kinetic energy, whereas larger eddies merely carry cells along convectively (8–12).

Table 1: Comparison of parameters used for calculating hydrodynamic stress in two

different 1000-L single-use bioreactors (adapted from Reference 2)

Mixing in Bioreactors.

¹ from Cytiva ² from Thermo Fisher Scientific

* Maximum values during a process at the current bioreactor size ** Calculated from EDR mean

Mixing is a physical operation that reduces nonuniformities in fluid by eliminating gradients of temperature, concentration, and other properties (1). During mixing, material interchanging among different locations of a vessel (such as a mixing container or a bioreactor) causes components to “mingle.” Mixing is widely used in bioprocessing for

• blending soluble components of powder media in water to prepare for cell culture

• dispersing gases such as air and oxygen through liquids in the form of bubbles

• maintaining suspension of solid particles such as cells or cellular aggregates (e.g., on microcarriers)

• promoting heat transfer to or from liquids.

Mixing is one of the most important unit operations in bioprocessing. It is not enough to just fill a bioreactor with nutrient-rich media and cells. Unless the contents of that bioreactor are mixed, cells will settle, and zones of nutrient depletion will develop as they rapidly consume the material they need within their local environment. Mixing controls their access to dissolved nutrients and oxygen while playing a critical role in controlling culture temperature. Mixing equipment has a significant effect on agitation efficiency, directly affecting power requirements and operating costs. Development of hydrodynamic forces in media and other fluids drives aeration processes such as gas-bubble break-up, gas hold-up, and uniform dispersion of bubbles. Thus, mixing can determine the success a bioprocess.

Bioreactor Geometry: Most stainless-steel (or reusable) large-scale bioreactors are cylindrical, with a ratio of tank height to diameter (H/T) >1 (Figure 2). Baffles — cylindrical metal strips — are mounted against a bioreactor wall to reduce gross vortexing and swirling in the liquid. Mixing is achieved by means of an impeller mounted on a centrally located stirrer shaft driven by a motor. The rotating impeller pumps and forces liquid away from it, creating a regular flow pattern that circulates through the vessel and periodically returns to the impeller region. For aeration, gas (usually air and/or oxygen) is introduced into the vessel by means of a sparger located beneath the impeller. A headspace typically falls in the range of 20–30% of total vessel volume for cylindrical bioreactors.

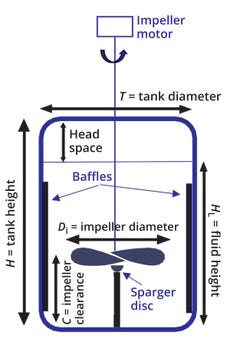
Figure 2: Dimensions of mixing-related components in a bioreactor.

The shape of the base of a stirred tank affects mixing efficiency. Most stirred bioreactors have a rounded rather than a flat base, preventing sharp corners and pockets into which fluid currents could penetrate, and thus discouraging the formation of stagnant zones. The energy required to keep solids (such as cells) suspended in a stirred tank also depends on the shape of the vessel base. For efficient mixing with a single impeller, the impeller diameter (D_i) should fall between 0.25 and 0.50 of the tank diameter (T), and the liquid height (H_L) should fall within 1.0 and 1.25 of T. That’s because mixing intensity decreases rapidly as fluid moves away from the impeller zone, so large liquid volumes in the upper parts of a vessel (away from the impeller) are difficult to mix — and thus should be prevented. Another aspect of vessel geometry that influences mixing efficiency is the clearance (C) between the impeller and the tank bottom, which affects solids suspension, gas dispersion, and hydrodynamic stability. For most stirred bioreactor systems, the ratio of clearance to fluid height (C/H_L) typically falls into the range of 0.33–0.66 (3).

Impeller type is critical to bioreactor design. An impeller system must be able to impart enough power into the cell culture medium for enabling good mixing efficiency, homogeneity, and sufficient mass transfer to satisfy cellular oxygen demand. Figure 3 shows two of the most common impeller designs used in both reusable and single-use bioreactors: Rushton and pitched-blade impellers. When the blade (or paddle) of an impeller rotates, it pushes the adjacent fluid. That action creates a high-pressure region on the front face and a low-pressure region immediately behind the blade (or paddle). Those regions are responsible for fluid motion inside a bioreactor and eventually for fluid mixing. Fluid located away from the impeller generally remains at a constant pressure.

Figure 3: Pitched-blade and paddle (Rushton) impellers commonly used in bioreactors (adapted from Reference 3).

Fluid velocity is highest at the tip of a rotating blade (or paddle), and it rapidly decreases away from the impeller. As it rotates, the impeller induces rotational velocity in the surrounding fluid, which can be observed by the high velocity region next to the impeller. Rushton impeller paddles also induce radially outward flow in nearby regions. It pulls liquid from top and bottom regions of a bioreactor, which creates a circular motion inside the vessel. That motion enhances fluid mixing. By contrast, pitched-blade impellers create mainly an axial flow (from top to bottom).

The preferred impeller design for cell-culture bioreactors uses pitched blades (with optimal blade diameter and agitation speed) because paddles are more likely to cause shear damage. Pitched-blade impellers primarily generate axial flow, but with appropriate blade configuration they also can balance both axial and radial flow patterns (4, 5).

Axial flow is necessary for top-to-bottom mixing in a stirred-tank bioreactor, and pitched-blade impellers (with blades angled <90° to the plane of rotation) can generate such flow efficiently. As Figure 4 shows, fluid leaving an impeller is driven downwards until it is deflected from the bottom of the vessel. Then the fluid spreads out and flows up along the vessel walls before it is drawn back to the impeller. The rotational flow makes baffles necessary to break down vortex formation along the vessel walls.

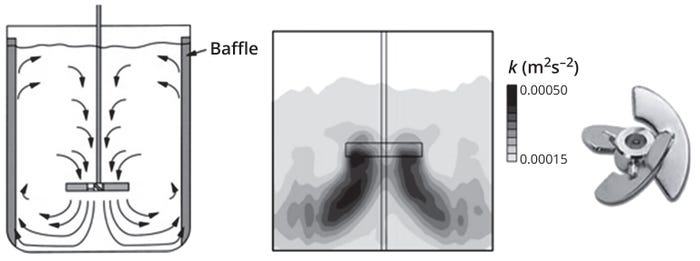
Figure 4: The axial flow pattern induced by pitched blade impellers (left) and the turbulent kinetic energy distribution profile of a pitched-blade impeller (right) generated by computational fluid dynamics (CFD) simulation (adapted from Reference 1).

A pitched-blade impeller agitating at sufficiently high velocity in a low-viscosity medium (e.g., water and cell culture media) generates a turbulent region of high shear and rapid mixing near the impeller. That high-shear region is responsible for bubble break-up in sparged bioreactors. As Figure 4 shows, the distribution of turbulent kinetic energy is not uniform throughout the tank, with the highest values mostly occurring in a region close to the impeller. Levels of turbulent kinetic energy in the remainder of the tank away from the impeller are up to an order of magnitude lower than the maximum values measured (1).

Axial flow is useful when strong vertical currents are required — e.g., to suspend solids or cells in fluid. The ability to operate a pitched-blade impeller in either up-flow or down-flow mode is an important requirement that can be provided by a bidirectional motor. For most animal cell-culture systems, these impellers are programmed for up-flow pumping mode. However, the down-flow option can be useful for enabling suspension of adherent-cell cultures on microcarriers at low speeds with low specific power input to prevent shearing the cells from their carriers (3).

Disc-mounted impellers with six flat blades, commonly known as Rushton turbines, generate radial flow (Figure 5). They are used frequently in microbial fermentation, for which they can generate very high shear and thus provide effective gas dispersion. A Rushton turbine generates a jet of high-speed flow radially outward from the impeller toward the walls of the tank.

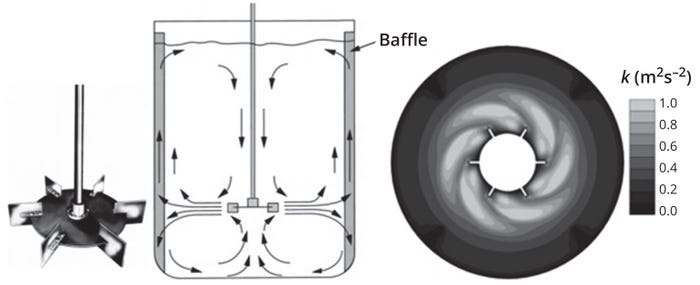
Figure 5: The radial flow pattern induced by Rushton impellers (left) and their turbulent kinetic energy distribution profile (right) generated by computational fluid dynamics (CFD) simulation (adapted from Reference 1).

That fluid stream gets divided in half, with one stream flowing up and the other down toward the tank bottom. Bulk flow in the vessel thus comprises two large ring vortices, one above and the other below the impeller.

Another characteristic of Rushton turbines is their generation of trailing vortices in fluid behind the horizontal edges of each flat impeller blade (Figure 5). The vortices play a critical role to determine mixing performance because most mixing takes place near the vortices issuing from the impeller blades. These trailing vortices also provide gas dispersion in sparged systems. The associated steep velocity gradients provide a major source of turbulence. One reason for widespread use of Rushton turbines in microbial fermentors is their ability to handle high gas-flow rates and provide efficient gas dispersal.

The power required to achieve a given stirrer speed depends on frictional forces and form drag (caused by the pressure difference between the front and rear of the impeller blades) that resists impeller rotation. Friction and form drag create torque on the stirrer shaft. The power input can be determined experimentally by measuring the induced torque (Equation 4):

P = 2πN_iM

where P is the power, N_i is the stirrer speed, and M is the torque.

The power required to mix nongassed liquids depends on stirrer speed, impeller shape and size, tank geometry, and liquid density and viscosity. The relationships among those variables generally is represented by the dimensionless power number (Equation 5):

N_P = P/ρN_i³D_i⁵

where N_P is the power number, P is the power, N_i is the stirrer speed, and D_i is the impeller diameter.

Consider the power number as analogous to a drag coefficient for a stirrer system. The relationship between N_P and Re generally is determined experimentally for a range of impeller and tank configurations. The power number for different impeller designs becomes constant once flow is turbulent (1). Under turbulent flow conditions in a stirred tank, the power number for a Rushton turbine generally remains constant at 5, whereas that of an axial pitched-blade impeller is about 1. Thus, a Rushton turbine has strong form drag, generates high levels of torque, and transmits more power at the same operating speed than does a pitched blade impeller (1).

Fluid Flow: Rotating impeller blades pump fluid in a bioreactor vessel. The volumetric flow rate of fluid leaving a blade is a characteristic of the impeller design and varies with operating parameters such as stirrer speed and blade size. A dimensionless flow number represents the effectiveness of a pumping process (Equation 6):

N_flow = Q/N_iD_i³

where Q is the volumetric flow rate of fluid leaving the impeller blade, N_i is the stirrer speed, and D_i is the impeller diameter.

A pitched-blade impeller produces nearly three to four times the flow of a Rushton turbine for the same power input. This is why the former design is recognized for high pumping capacity and effectiveness of blending operations, whereas the latter are considered to have low pumping efficiency (1).

For mixing to be effective in stirred vessels, the velocity of fluid leaving an impeller must be sufficient to carry material into the most remote regions of a tank. Circulating fluid also must sweep the entire vessel in a reasonable time. Fluid flow must be turbulent for good mixing, which can be described as a combination of three physical processes (1): distribution, dispersion, and diffusion. Distribution is also called “macromixing,” diffusion is known as “micromixing,” and depending on the scale of fluid motion, dispersion can be classified as either macro- or micromixing.

Distribution is the process by which fluid is transported to all regions of a stirred vessel by bulk circulation currents. It is an important process in mixing and often the slowest step because fluid has a great distance to traverse in a long circulation path. Dispersion breaks up the bulk flow into smaller and smaller eddies, which facilitates rapid transfer of material through a vessel. The degree of homogeneity possible from dispersion is limited by the size of the smallest eddies formed in a particular fluid. To achieve mixing on a scale smaller than the smallest eddies, diffusion becomes an important process. Such micromixing occurs relatively rapidly and over shorter distances than are involved in distribution.

Mixing time (t_m) is a useful parameter for assessing the overall speed of mixing in stirred vessels. It is the time required to achieve a given degree of homogeneity after starting with completely segregated materials. Mixing time can be measured by injecting tracer material — commonly acids, bases, or concentrated salt solutions — into a vessel and following its concentration at a fixed point in the tank.

When a small pulse of tracer is added to fluid in a stirred tank that already contains the tracer material at a certain concentration (C_i), the concentration response curve in Figure 6 can be expected. Before mixing is complete, a relatively high concentration will be detected each time the bulk flow brings tracer to the measurement point. The resulting peaks in concentration will be separated by a period approximately equal to the average time required for fluid to traverse one bulk circulation loop, known as the circulation time (t_c). After several circulations, a desired degree of homogeneity will be achieved.

Figure 6: Determination of mixing time (t_m) by following the concentration (C) response

after a tracer dye is injected into a stirred tank (adapted from Reference 1); C_f = final

concentration, C_i = interim concentration, t_c = circulation time.

Mixing time generally is expressed as the time after which the tracer concentration differs from its final concentration (C_f) by <5–10% of the total concentration difference (C_f – C_i). At t_m, the tracer concentration is relatively steady, and the fluid composition approaches uniformity. For industrial-scale bioreactors, that takes minutes.

Liquid-phase mixing is vitally important in large-scale bioreactors because feed components, bases, or antifoam detergents are added, in most cases, at the top surface of the fluid (12, 13). Such added materials must be distributed quickly throughout an entire culture to reach homogeneity without causing localized concentration gradients. The homogenization process is dominated by prevailing flow patterns, and information about global mixing conditions in a bioreactor can be obtained from t_m measurements.

Sieblist et al. reported such a study of large-scale bioreactors, determining t_m using an iodine-decolorization technique (14). The data in Figure 7, obtained using three Rushton turbines and three pitched-blade impellers, show that at the same power input the spatial decolorization patterns and speed of decolorization are very different for those agitator types. Those results provide experimental evidence that impellers inducing axial flow reduce t_m by about a factor of two. The reason for that is their notably improved top-to-bottom mixing due to a more widescale flow structure induced by the axially down-pumping pitched-blade impellers; Rushton turbines induce flow compartmentalization, leading to less efficient overall mixing and hence longer mixing times.

Figure 7: Determination of mixing time (t_m) in a 400-L bioreactor fitted with either

three Rushton turbines (circles) or three pitch-blade impellers (triangles) (adapted from

Reference 14); data are fitted to the correlation reported by Ruszkowski (15); D =

impeller diameter, H = tank height, T = tank diameter, ε = the local rate of turbulent

energy dissipation per unit mass of the fluid, θ_95% = time needed to reach 95%

homogeneity in the bioreactor.

A striking finding from that study is that mixing time depends only on bioreactor geometry rather than the agitation system. Different impeller configurations influence the constant factor (10.5 or 17.9) in the empirical correlation of Ruszkowski (15). Another experiment reported by Sieblist et al. demonstrated that mixing times critically depend on experimental conditions, particularly the location in the bioreactor where the tracer is added (14). Figure 8 shows that the effect of adding tracer close to the impeller is much larger than that at the reference point (the liquid surface), leading to shorter mixing times. That indicates the importance adding substrates and corrective agents (e.g., bases and antifoams) to cultures close to impellers, thus enabling rapid distribution to an entire culture. That implication has been understood for a long time; however, it is not general practice.

Figure 8: Mixing times measured in a 400-L stirred bioreactor at 90 W/m³ with tracer

added to the system at different points (adapted from Reference 14); numbers on the

bars show the difference in mixing time compared with a reference addition at the top

of the liquid surface; θ_95% = time needed to reach 95% homogeneity in the bioreactor.

The product of mixing time and stirrer speed (N_i · t_m) is known commonly as dimensionless mixing time, which represents the number of stirrer rotations required to homogenize a fluid after addition of a tracer pulse. For turbulent flow conditions in a bioreactor, N_i · t_m approaches a constant value for most stirrer types, and mixing time reduces in direct proportion to increasing stirrer speed. Under turbulent flow conditions, t_m can be reduced by increasing D_i. However, larger-diameter impellers also require more power consumption, so a tradeoff balance is needed when using that strategy for improving mixing and shortening mixing time.

Power requirements should be kept in mind for scaling up mixing systems. The power required to achieve a given mixing time for a larger bioreactor can be computed from Equation 7 (1):

P₂ = P₁(V_L2/V_L1)^5/3

where P₂ is the power required for the larger bioreactor, V_L2 is the liquid volume of the larger bioreactor, P₁ is the power required for the smaller bioreactor, and V_L1 is the liquid volume of the smaller bioreactor. For example, consider scaling up from a 1-L to a 100-L bioreactor: P₂ = P₁ × (100/1)^5/3 and P₂ = P₁ × 2155. Hence, the power required to achieve equal mixing times in the larger bioreactor would be ~2000× that of the smaller bioreactor. That is much greater than would be feasible economically or technically, illustrating why the criterion of constant mixing time seldom is applied in scaling up. Mixing time inevitably must increase with scale-up.

Installation of multiple impellers on the same stirrer shaft might be perceived as a simple solution to improve mixing in a bioreactor. However, the power required increases substantially when additional impellers are fitted onto the same shaft. Moreover, impeller design (axial or radial) and clearance between impellers significantly affects mixing performance and would need to be optimized to realize an improvement in overall efficiency.

References

Note: To refer back to part 1, see Chaudhry MA. Lessons in Bioreactor Scale-Up, Part 1: Exploring Introductory Principles. BioProcess Int. 22(1–2) 2024: 22–27; https://www.bioprocessintl.com/bioreactors/lessons-in-bioreactor-scale-up-part-1-mdash-exploring-introductory-principles.

1 Doran PM. Fluid Flow. Bioprocess Engineering Principles, 2nd Edition. Academic Press: Cambridge, MA, 2013: 201–254.

2 Minow B, et al. Biological Performance of Two Different 1000 L Single-Use Bioreactors Applying a Simple Transfer Approach. Eng. Life Sci. 14(3) 2014: 283–291; https://doi.org/10.1002/elsc.201300147.

3 De Wilde D, et al. Bridging the Gap from Reusable to Single-Use Manufacturing with Stirred, Single-Use Bioreactors. BioProcess Int. 7(4) 2009: 36–41; https://www.bioprocessintl.com/single-use/bridging-the-gap-from-reusable-to-single-use- anufacturing-with-stirred-single-use-bioreactors.

4 Nienow AW, Isailovic B, Barrett TA. Design and Performance of Single-Use Stirred-Tank Bioreactors. BioProcess Int. 14(11–12) 2016: 12–21; https://www.bioprocessintl.com/single-use/design-and-performance-of-single-use-stirred-tank-bioreactors.

5 Nienow AW. Reactor Engineering in Large-Scale Animal Cell Culture. Cytotechnology 50(1–3) 2006: 9–33; https://doi.org/10.1007/s10616-006-9005-8.

6 Nienow AW. Impeller Selection for Animal Cell Culture. Encyclopedia of Industrial Biotechnology: Bioprocess, Bioseparation, and Cell Technology. Flickinger MC, Ed. Wiley: Hoboken, NJ, 2010; https://doi.org/10.1002/9780470054581.

7 Godoy-Silva R, et al. Physiological Responses of CHO Cells to Repetitive Hydrodynamic Stress. Biotechnol. Bioeng. 103(6) 2009: 1103–1117; https://doi.org/10.1002/bit.22339.

8 Chisti Y. Hydrodynamic Damage to Animal Cells. Crit. Rev. Biotechnol. 21(2) 2001: 67–110; https://doi.org/10.1080/20013891081692.

9 Kunas KT, Papoutsakis ET. Damage Mechanisms of Suspended Animal Cells in Agitated Bioreactors with and without Bubble Entrainment. Biotechnol. Bioeng. 36(5) 1990: 476–483; https://doi.org/10.1002/bit.260360507.

10 Jossen V, et al. Stirred Bioreactors: Current State and Developments, with Special Emphasis on Biopharmaceutical Production Processes. Current Developments in Biotechnology and Bioengineering: Bioprocesses, Bioreactors, and Control. Larroche C, et al., Eds. Elsevier: Amsterdam, Netherlands, 2017: 179–215.

11 Palomares LA, Ramirez OT. Bioreactor Scale-Up. Encyclopedia of Industrial Biotechnology: Bioprocess, Bioseparation, and Cell Technology. Flickinger MC, Ed. Wiley: Hoboken, NJ, 2009; https://doi.org/10.1002/9780470054581.

12 Marks DM. Equipment Design Considerations for Large Scale Cell Culture. Cytotechnology 42(1) 2003: 21–33; https://doi.org/10.1023/A:1026103405618.

13 Langheinrich C, Nienow, AW. Control of pH in Large-Scale, Free Suspension Animal Cell Bioreactors: Alkali Addition and pH Excursions. Biotechnol. Bioeng. 66(3) 1999: 171–179; https://doi.org/10.1002/(sici)1097-0290(1999)66:3<171::aid-bit5>3.0.co;2-t.

14 Sieblist C, et al. Insights into Large-Scale Cell-Culture Reactors: I. Liquid Mixing and Oxygen Supply. Biotechnol. J. 6(12) 2011: 1532–1546; https://doi.org/10.1002/biot.201000408.

15 Ruszkowski S. A Rational Method for Measuring Blending Performance and Comparison of Different Impeller Types. Eighth European Conference on Mixing. Institution of Chemical Engineers: Rugby, UK, 1994: 283–291.

Further Reading

Mirro R, Voll K. Which Impeller Is Right for Your Cell Line? BioProcess Int. 7(1) 2009: 52–57; https://www.bioprocessintl.com/cell-line-development/which-impeller-is-right-for-your-cell-line-.

Dhanesekharan K. Design and Scale-Up of Bioreactors Using Computer Simulations. BioProcess Int. 3(4) 2006: 34–40; https://www.bioprocessintl.com/information-technology/design-and-scale-up-of-bioreactors-using-computer-simulations.

Platas Barradas O, et al. Evaluation of Criteria for Bioreactor Comparison and Operation Standardization for Mammalian Cell Culture. Eng. Life Sci. 12(5) 2012: 518–528; https://doi.org/10.1002/elsc.201100163.

Schirmer C, et al. Development, Engineering and Biological Characterization of Stirred Tank Bioreactors. Biopharmaceuticals. Yeh M-K, Ed. IntechOpen: London, UK, 2018; https://dx.doi.org/10.5772/intechopen.79444.

A seasoned industry professional with a PhD in chemical and biological engineering from the University of British Columbia (Vancouver, Canada) and expertise in embryonic stem cell bioengineering, upstream biological process development, and fed-batch bioreactors, Muhammad Arshad Chaudhry is associate director of process and formulation development at Mural Oncology, 852 Winter Street, Waltham, MA 02451; [email protected].