Lessons in Bioreactor Scale-Up, Part 5: Theoretical and Empirical Correlations for Predicting the Mass-Transfer Coefficient in Stirred-Tank BioreactorsLessons in Bioreactor Scale-Up, Part 5: Theoretical and Empirical Correlations for Predicting the Mass-Transfer Coefficient in Stirred-Tank Bioreactors

HTTPS://STOCK.ADOBE.COM

A primary difficulty associated with scaling up cell-culture bioreactors involves prediction of physiological conditions in target vessels. As discussed earlier in this series, oxygen availability — characterized by its rate of transfer to the culture liquid (oxygen transfer rate, OTR) and its consumption by cells (oxygen uptake rate, OUR) — is critical to proper cell function and production of desired proteins. Cellular respiration and production in a large-scale bioreactor depend on maintaining adequate oxygen levels throughout the bioreactor without any gradients.

In a stirred-tank bioreactor (STR), a gas or a mixture of gases often is sparged through the liquid as bubbles. Fractional gas hold-up in the bioreactor is the primary measure of gas–liquid contact efficiency. Hence, gas hold-up (Φ) and mean bubble diameter (d_b) determine the gas–liquid mass-transfer area. In turn, the most important characteristics affecting mass transfer between gas and liquid phases in an STR are

• gas hold-up (Φ values)

• bubble size or bubble-size distribution (often based on d_b values)

• kinetic energy dissipated per unit mass by turbulence (ε).

Those parameters depend on bioreactor operating conditions (e.g., power input or stirred speed and gas flow rate), culture-broth physicochemistry (density, viscosity, and surface tension), and bioreactor and sparger geometry. All of these factors are interrelated; hence, STR design and scale-up are difficult, multiparametric considerations.

Theoretical Prediction of the Mass-Transfer Coefficient

The volumetric mass-transfer coefficient (k_La) determines the rate at which a gaseous component, such as oxygen or carbon dioxide, can transfer between gas and liquid phases in a given culture environment. The k_L part of the coefficient essentially represents the rate of molecular diffusion through the gas–liquid interface, and a represents the interface area that is available for mass transfer per liquid volume.

Over the past few decades, academic and industry scientists have conducted extensive research on oxygen transfer in bioreactors and its dependence on different physicochemical and process parameters. From such studies have come a considerable amount of published experimental data and a variety of theoretical correlations. Below, I overview this vast field of research as it relates to large-scale STRs.

Theoretical models for k_L prediction can be divided by approach. Some early models were based on the two-film theory and later on the concept of surface renewal (1). Higbie’s penetration theory is a widely accepted description of gas–liquid mass transfer, and several models have been developed based on that concept (2–5). Assuming nonstationary diffusion at a gas–liquid interface during contact (the exposure time for mass transfer, te), a theoretical model for k_L can be obtained (Equation 1). Therein, the variable D_L represents the diffusion coefficient of oxygen in the liquid.

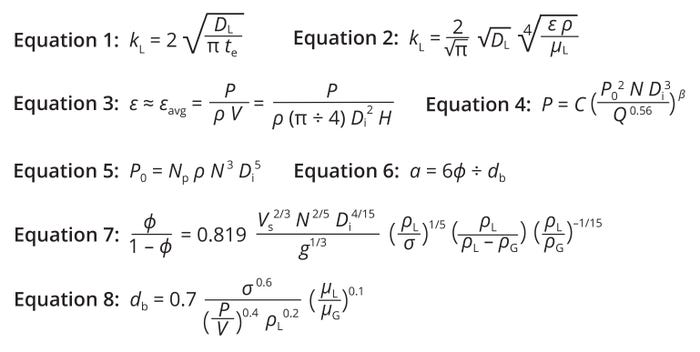
^{Equations 1–8: Theoretical prediction of the oxygen mass-transfer coefficient (k}L^{) and interfacial area (a) for stirred-tank bioreactors.}

It has been shown that k_L depends on turbulent intensity, expressed as a function of ε. Experimental results also have demonstrated that microscopic-scale eddies can influence t_e values. Hence, according to Kolmogoroff’s theory of isotropic turbulence, t_e is assumed to be proportional to the amount of time for a bubble to rise one bubble diameter. As a result, t_e can be determined as a ratio of bubble diameter to bubble-rise velocity (t_e = d_B/U_B). Those two latter parameters depend on ε and kinematic viscosity (ν), respectively. Hence, for Newtonian fluids, Equation 2 enables theoretical prediction of k_L values (6, 7).

Because k_L depends on local, turbulent, dissipated kinetic energy near the gas–liquid interface, ε needs to be estimated. Energy at the interface is assumed to be consumed at the contact between the liquid elements and gas bubbles. Estimation of ε at the interface is essentially impossible; hence, the average kinetic energy dissipated per unit mass (ε_avg) in an STR serves as a surrogate value. For aerated (sparged) systems, that value is captured by Equation 3, in which P represents power consumed in the aerated tank, D_i is the stirrer diameter, and H is the liquid height. The value of aerated power P is always less than that for nonaerated (or ungassed) power P₀ consumed (Figure 1).

^{Figure 1: The ratio of gassed power to ungassed power (P/P}0^{) drawn by a Rushton turbine impeller in a 10-m3 cellculture bioreactor as a function of stirrer speed and aeration rate; for a given impeller speed, the P/P}0 ^{ratio decreases with increasing aeration rate and vice versa.}

^{(ADAPTED FROM 10)}

For STRs, those power values are related by Equation 4, which was proposed by Michel and Miller (8). Therein, N represents the stirrer speed (in revolutions per second), and Q is the gas flow rate (m³/s). For single-impeller systems, the constants C and β equal 0.783 and 0.459, respectively. For dual-impeller systems, those values are 1.224 and 0.432. Ungassed power consumption in a stirred tank, P₀, can be estimated using Equation 5, in which N_p represents the impeller power number.

Calculating the overall mass-transfer coefficient requires estimation of the interfacial area, a, which is a function of vessel geometry and prevailing hydrodynamic conditions. Assuming spherical bubbles, a can be calculated from the mean bubble size, d_b, and gas hold-up, Φ, as shown in Equation 6. Equations 7 and 8 enable calculation of values for those variables. Therein, g represents acceleration due to gravity, ρ_L denotes the liquid density (in kg/m³), ρ_G is the gas density (in kg/m³), and σ is the interfacial surface tension (in N/m).

Empirical Correlations for k_La Prediction

The value of k_La in a cell-culture broth depends on fluid properties and prevailing hydrodynamic conditions in an STR. By determining factors that directly influence oxygen solubility and dispersion, researchers have developed mostly empirical models for k_La prediction in a variety of gas–liquid contacting systems, including STRs.

A review of literature on mass transfer coefficients reveals three common methods for predicting k_La (9):

• correlations based on an energy-input criterion — this is the most frequently used method, one that relates k_La to power input (P/V) and the superficial gas velocity (V_s)

• correlations based on dimensionless numbers — this method relates k_La to Froude’s number (Fr), the gas flow number (Fl_G), and the ratio of impeller to tank diameters (D_i/T)

• correlations based on relative gas dispersion (N/N_cd), with N_cd representing the minimum impeller speed required for all culture liquid to be in contact with sparged gas.

Correlations Based on Energy Input: Over the past few decades, researchers have tested extensively the dependence of STR oxygen k_La on both fluid properties (e.g., oxygen diffusivity and liquid density, viscosity, and surface tension) and prevailing hydrodynamic conditions (fluid velocity, gas hold-up, gas flow rate, and bubble diameter). Results from such studies generally have yielded empirically derived correlations between k_La and important STR operating parameters. In principle, such correlations allow for k_La prediction based on information gathered from a large number of experiments performed in similar systems under similar conditions. In practice, such correlations generally have shown poor accuracy.

The chief reason that such correlations do not apply to biological systems is that oxygen transfer depends strongly on the variety of additives included in a cell-culture or fermentation medium — from sugars to amino acids, vitamins, trace metal salts, and surfactants. The surface chemistry of gas bubbles, and therefore the mass-transfer situation, in a bioreactor is extremely complex. Most theoretical correlations were developed using air in water as a model system. The presence of additives in a culture medium affects the value of k_La so significantly that making corrections to published correlations based on different liquid compositions is nearly impossible. The presence of cells and other culture-broth components also influences the interfacial area for mass transfer, a, complicating development of a predictive k_La correlation that has general applicability.

Another factor that limits the application of empirical k_La correlations to large-volume bioreactors relates to the difference in prevailing hydrodynamic conditions across scales. Most theoretical k_La correlations were developed using laboratory-scale bioreactors, in which intense turbulent flow conditions are realized throughout the vessel. By contrast, intense turbulence in a large-scale bioreactor is limited to the impeller region; flow in the remainder of the vessel is much slower. Due to such differences in hydrodynamic regimes, the mass-transfer correlations developed using laboratory-scale bioreactors tend to overestimate the oxygen-transfer capacity of commercial-scale systems.

Nonetheless, a general consensus has emerged about the form of the equation that relates oxygen k_La to bioreactor operating conditions. For most bioreactor configurations, k_La is correlated mainly to

• volumetric power input, P/V, a measure of turbulent kinetic energy dissipation in a bioreactor

• superficial gas velocity, V_s, the gas flow rate for a cross-sectional area of bioreactor.

Equation 9 — also known as van’t Riet’s correlation — shows the general form of that correlation (11). The constant K varies significantly with a liquid’s composition and is sensitive to coalescing properties and the presence of cells. The values of constants α and β, on the other hand, are largely insensitive to culture-broth properties and generally fall in the range of 0.2 to 1.0 (12). Because both α and β are typically <1, increasing k_La by raising either the air flow rate or power input becomes progressively less efficient and more costly.

^{Equations 9–16: Empirical correlations for prediction of the volumetric oxygen masstransfer coefficient (k}L^{a ) for stirred-tank bioreactors.}

A useful study by Pappenreiter et al. reported k_La measurement in a 15-L (working volume) bioreactor system as a function of temperature, stirrer speed, and process air-flow rates (Figure 2a) (12). Process air-flow and stirrer-speed variations were linked through the proportional–integral–derivative (PID) controller’s output (Figure 2b), and their combined influence on k_La was quantified based on the percentage of controller output. The maximum controller output of 65% corresponded to a stirrer speed of 160 rpm.

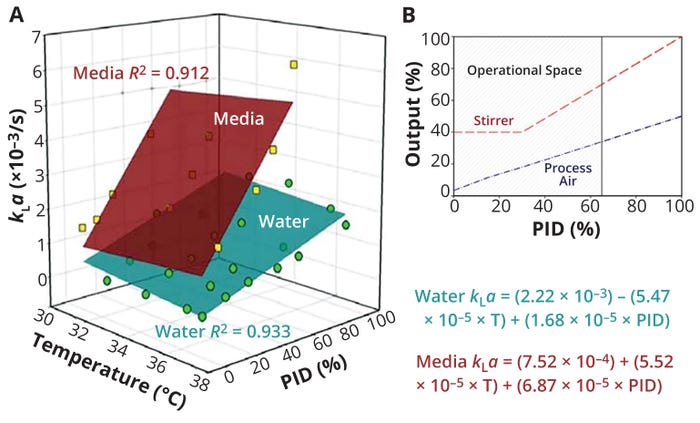
^{Figure 2: Results from Pappenreiter et al. (11); (a) volumetric oxygen mass-transfer (k}L^{a) as a function of temperature (T) and proportional–integral–derivative (PID) controller output (%) for water and a culture medium, both supplemented with 0.1% antifoam solution in a 15-L (working volume) bioreactor; (b) experimental design space showing stirrer and process-air outputs that were used in the study; the maximum controller output (PID%) was set to 65%. (ADAPTED FROM 11)}

The data plotted in Figure 1a show that culture temperature generated little to no observable effect on kLa. Moreover, the culture medium’s physicochemical properties exhibited a strong, positive influence on k_La , resulting in clearly superior (on average 3× higher) k_La values to those generated when testing water alone. Hence, using water as a substitute for culture media, as has been done in many previous studies, is inappropriate because it underestimates k_La values during culture processes.

Sieblist et al. explored k_La as a function of specific power input and aeration rate for a 400-L cell-culture bioreactor (Figure 3) (10). Measurements were performed in an electrolyte solution with osmolality adjusted to 300 mOsm/kg. Researchers operated the bioreactor with two different impeller setups, comparing Rushton and pitched-blade impellers in one- and three-impeller configurations to explore the dependence of k_La on specific power input imparted to the liquid by each impeller set at different aeration rates.

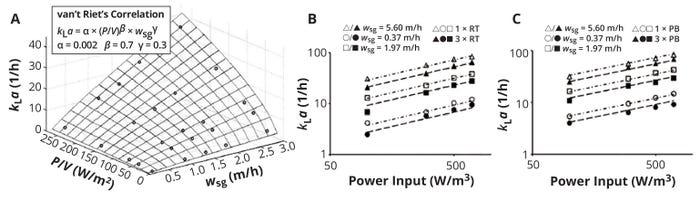
^{Figure 3: Volumetric oxygen mass-transfer coefficient (k}L^{a) as a function of superficial gas velocity (V}s^{) and specific power input induced by an impeller system; (a) experimental k}L^{a data fitted to van’t Riet’s correlation (Equation 9); (b) comparison of k}L^{a values for a 400-L cell-culture bioreactor equipped with one (open symbols) or three (closed symbols) Rushton turbines; (c) comparison of k}L^{a values for a 400-L bioreactor equipped with one (open symbols) or three (closed symbols) pitched-blade impellers (ADAPTED FROM 10)}

The experimental k_La data generated during the study fit nicely with van’t Riet’s correlation. Figures 3b and 3c show those data as double-logarithmic plots. The linear relationships depicted indicate that k_La dependence on specific power input is exponential and that high aeration rates lead to high k_La values.

Another important observation from this data set involves the influence of impeller numbers on resulting k_La values. Compared with results from three-impeller configurations, use of a single impeller increased k_La for both Rushton and pitched-blade styles while keeping both volumetric power input and gas flow rate constant. That important finding suggests that, for a culture to achieve high kLa values, power input to a bioreactor must be concentrated to the area where bubbles are being generated: close to the impeller region, where turbulence is most intense. Thus, local turbulent power dissipation density, ε_max, is more important to mass transfer than is the average (or integral) power transferred to the reactor liquid.

Gill et al. have compiled a summary of the most commonly reported k_La correlations for STRs of different sizes (Table 1) (13). Those and most other correlations available in the literature were derived for oxygen k_La in microbial fermentation systems with high energy input (agitation speeds) and aeration rates that generally are not used in cell-culture bioreactors. In addition, using theoretical k_La correlations based on energy-input criteria (e.g., Equation 9) for scale-up of cell-culture bioreactors is not recommended because those correlations’ constant and exponent values tend to be system-specific.

^{Table 1: Summary (adapted from 13) of oxygen mass-transfer coefficient (k}L^{a) correlations reported in published literature for stirred vessels of 0.002–206 m3; D/T = impeller diameter:tank diameter ratio, DT = disc turbine, RT = Rushton turbine.}

k_La Correlations Based on Dimensionless Numbers: Orbitally shaken bioreactors — shake flasks, spin tubes, cylindrical or square-shaped glass bottles, and even disposable orbitally-shaken bioreactors with integrated instruments —of up to 200 L have found increasing use in mammalian- and plant-cell culture operations. For example, shake flasks often serve as vessels for seed-train expansion during mammalian-cell culture. Such reactors also are used to test the effects of different culture conditions during screening of transfected pools and clonal cell lines.

As is the case with an STR, the k_La value of a shaken bioreactor is defined by liquid-phase physicochemical properties and shaking parameters. Considerable advances have been made over the past two decades in developing mathematical models to estimate k_La for shaken reactors (18–22). Scientists can use such models to compare values in geometrically similar shaken bioreactors of different scales.

Several operating and physiochemical parameters correlate with k_La in such systems — e.g., vessel diameter (d), shaker platform diameter (d₀), shaking frequency (n), filling volume (V_L), oxygen diffusion coefficient (D_O2), kinematic viscosity (ν), and gravitational acceleration (g). Dimensional analysis of such variables using the Buckingham π theory yields Equation 10, which contains the constant C as well as a set of dimensionless numbers: Fr, the volume number, the geometric number, the Galilei number (Ga), and the Schmidt number (Sc) (19, 21).

In Equation 10, exponents α–ε represent the influence of each dimensionless group. Values for those exponents are determined individually and empirically. The Fr term expresses the ratio of centrifugal to gravitational forces during shaking. Relative filling volume is considered with the volume number. The geometric number describes the ratio of shaking diameter to reactor diameter. The height and shape of the free liquid surface during shaking is influenced by the ratio of gravitational to viscous forces, expressed by Ga. Finally, Sc describes the ratio of momentum transfer to the diffusive mass transfer in the gas or liquid surface (19). In orbitally shaken bioreactors, the influence of surface tension on the mass-transfer coefficient decreases as the reactor size increases (20, 23). Hence, surface tension is not included in Equation 10.

In orbitally shaken bioreactors, a critical circulation frequency (N_C) is needed to induce rotational liquid motion. Below that frequency, nearly zero liquid movement would be observed between the bulk liquid and reactor wall (24). Equation 11 gives the value of N_C.

Klöckner et al. have provided values for the constant and exponents in Equation 10. The resulting Equation 12 can be used to calculate k_La for cylindrical, orbitally shaken bioreactors of 2 to 200 L (19). The same exponents for the Fr and geometric-number terms in Equation 12 eliminate the shaking-diameter value, yielding a simplified form shown in Equation 13. Therein, d refers to the influence of vessel diameter, n represents the shaking frequency, and V_L is for reactor working (or filled) volume — all process parameters. Variables representing physiochemical properties include ν for liquid viscosity and D_O2 for oxygen diffusivity. As in previous equations, g represents the influence of gravity. Equation 14 shows a similar correlation for shake flasks (21).

Zhu et al. have reported experimental k_La values for orbitally shaken bioreactors spanning 250 mL to 2500 L (25). Based on those data, the team also developed a theoretical model similar to Equation 12 to predict k_La values. Figure 4 compares the experimental and theoretical values. Zhu et al. found that Re values and interactions between Fr and geometric numbers have the largest positive impact on k_La values, whereas the volume number had the largest negative impact. The authors ultimately recommended either increasing the shaking speed or diameter or decreasing the reactor diameter to increase oxygen supply in orbitally shaken bioreactors.

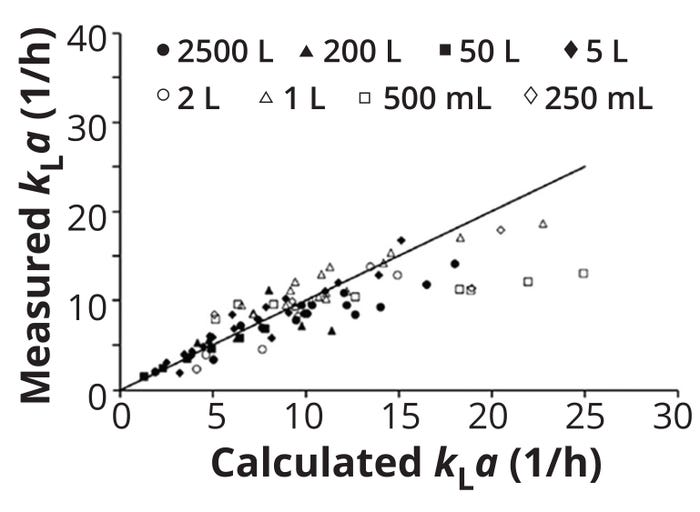
^{Figure 4: Comparison of measured and calculated values for the volumetric oxygen mass-transfer coefficient (k}L^{a) for orbitally shaken bioreactors operated at 37 °C, from 250-mL shake flasks to 2500-L bioreactors; a model similar to that shown in Equation 12 was used to predict theoretical k}L^{a values. (ADAPTED FROM 25)}

k_La Correlations Based on the Relative Gas-Dispersion Number: For economical gas–liquid mixing in an STR, the impeller must disperse sparged gas in the tank completely. Hence, process engineers must know the minimum impeller speed (N_cd) that results in complete dispersion of the gas phase in the liquid. Mixing at an impeller speed below the N_cd value, therefore, would result in incomplete gas dispersion. If little to no gas is in the region below the impeller, then the lower part of the STR is wasted in terms of gas–liquid mixing. Thus, N/N_cd is a dimensionless relative gas-dispersion parameter.

Nienow et al. have developed a correlation for N_cd in an STR equipped with a standard six-blade disc turbine (Equation 15) (26). Therein, Q_G signifies the volumetric gas-flow rate (in m³/s), T is a stirred tank’s inner diameter (m), and D_i is the impeller diameter (m).

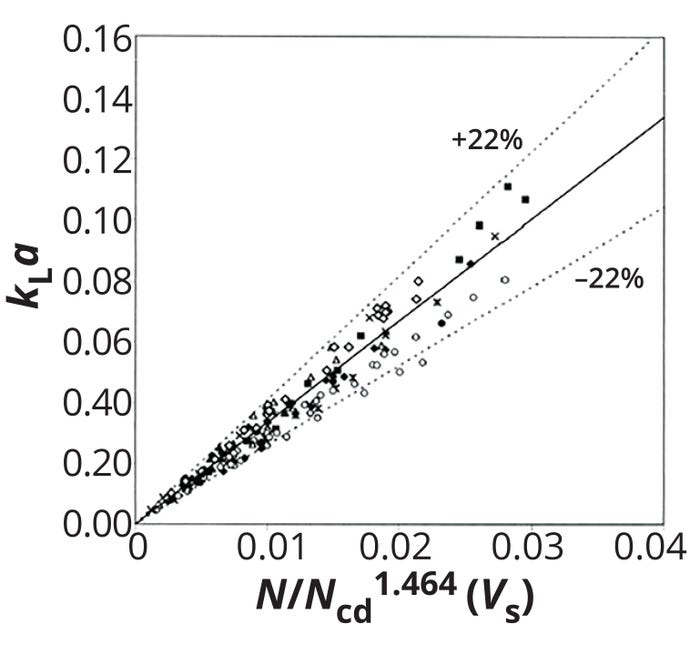
^{Figure 5: Comparison between exprimentally measured and calculated values for the volumetric oxygen masstransfer coefficient (k}L^{a) by Equation 16; N/N}cd ^{= relative dispersion number, V}s ^{= superficial gas volume (ADAPTED FROM 9)}

Yawalkar et al. similarly developed a k_La correlation based on a relative dispersion number, given by Equation 16 (9). The equation reliably fits an array of experimental k_La data, with a standard deviation of 22% (Figure 5). The team also compiled a list of other published k_La correlations based on N/N_cd(Table 2).

^{Table 2: Reported correlations for obtaining the oxygen mass-transfer coefficient (k}L^{a) based on relative dispersion number (N/N}cd^{); R2 = coefficient of variation, SE = standard error (TABLE ADAPTED FROM 9)}

Next in This Series

Part 6 of this series shifts the focus from oxygen to dissolved carbon dioxide, exploring its physiochemical properties, effects on mammalian-cell metabolism, and implications for cell-culture systems.

Variables and Constants for Determining the Volumetric Oxygen Mass-Transfer Coefficient (kLa)

a: interfacial area for mass transfer

d: orbital-shaker vessel diameter

d₀: orbital-shaker platform diameter

d_b: mean bubble diameter

D_i: impeller/stirrer diameter

D_L: oxygen diffusion coefficient

D_O2: oxygen diffusion (shaken bioreactor)

Fl_g: gas flow rate

Fr: Froude’s number

g: gravitational acceleration

Ga: Galilei number

H: liquid height in vessel

k_L: oxygen mass-transfer rate

n: shaking frequency

N: stirrer/impeller speed

N_C: critical circulation frequency

N_cd: minimum impeller speed required for complete mixing

N/N_cd: relative gas dispersion

N_p: impeller power number

P: aerated power input

P₀: nonaerated power input

Q: gas flow rate

Q_G: volumetric gas-flow rate

Sc: Schmidt number

t_e: exposure time for mass transfer

T: tank/vessel inner diameter

U_b: bubble-rise velocity

V: volume

V_L: filling volume

V_s: superficial gas velocity

ε: dissipated kinetic energy per unit mass

ε_avg: average dissipated kinetic energy

μ_L: liquid viscosity

ν: kinematic viscosity

ρ: density

ρ_L: liquid density

ρ_G: gas density

σ: interfacial surface tension

Φ: gas hold-up

Constants: a, C, K, β, γ, δ

References

1 Danckwerts PV. Significance of Liquid-Film Coefficients in Gas Absorption. Ind. Eng. Chem. 43(6) 1951: 1460–1467; https://doi.org/10.1021/ie50498a055.

2 Billet R, Schultes M. Predicting Mass Transfer in Packed Columns. Chem. Eng. Technol. 16(1) 1993: 1–9; https://doi.org/10.1002/ceat.270160102.

3 Kawase Y, Hashiguchi N. Gas–Liquid Mass Transfer in External-Loop Airlift Columns with Newtonian and Non-Newtonian Fluids. Chem. Eng. J. 62(1) 1996: 35–42; https://doi.org/10.1016/0923-0467(95)03049-2.

4 Kawase Y, Moo-Young M. Volumetric Mass Transfer Coefficients in Aerated Stirred Tank Reactors with Newtonian and Non-Newtonian Media. Chem. Eng. Res. Develop. 66, 1988: 284–288.

5 Tobajas M, et al. Hydrodynamics and Mass Transfer Prediction in a Three-Phase Airlift Reactor for Marine Sediment Biotreatment. Chem. Eng. Sci. 54(21) 1999: 5347–5354; https://doi.org/10.1016/S0009-2509(99)00262-6.

6 Garcia-Ochoa F, et al. Oxygen Uptake Rate in Microbial Processes: An Overview. Biochem. Eng. J. 49(3) 2010: 289–307; https://doi.org/10.1016/j.bej.2010.01.011.

7 Garcia-Ochoa F, Gomez E. Theoretical Prediction of Gas–Liquid Mass Transfer Coefficient, Specific Area and Hold-Up in Sparged Stirred Tanks. Chem. Eng. Sci. 59(12) 2004: 2489–2501; https://doi.org/10.1016/j.ces.2004.02.009.

8 Michel BJ, Miller SA. Power Requirements of Gas–Liquid Agitated Systems. AIChE J. 8(2) 1962: 262–267; https://doi.org/10.1002/aic.690080226.

9 Yawalkar AA, et al. Gas–Liquid Mass Transfer Coefficient in Stirred Tank Reactors. Can. J. Chem. Eng. 80(5) 2002: 840–848; https://doi.org/10.1002/cjce.5450800507.

10 Sieblist C, et al. Insights into Large-Scale Cell-Culture Reactors: I — Liquid Mixing and Oxygen Supply. Biotechnol. J. 6(12) 2011: 1532–1546; https://doi.org/10.1002/biot.201000408.

11 van’t Reit K. Review of Measuring Methods and Results in Nonviscous Gas-Liquid Mass Transfer in Stirred Vessels. Ind. Eng. Chem. Process Des. Dev. 18(3) 1979: 357–364; https://doi.org/10.1021/i260071a001.

12 Pappenreiter M, et al. Oxygen Uptake Rate Soft-Sensing via Dynamic kLa Computation: Cell Volume and Metabolic Transition Prediction in Mammalian Bioprocesses. Front. Bioeng. Biotechnol. 7, 2019; https://doi.org/10.3389/fbioe.2019.00195.

13 Gill NK, et al. Quantification of Power Consumption and Oxygen Transfer Characteristics of a Stirred Miniature Bioreactor for Predictive Fermentation Scale-Up. Biotech. Bioeng. 100(6) 2008: 1144–1155; https://doi.org/10.1002/bit.21852.

14 Vilaça PR, et al. Determination of Power Consumption and Volumetric Oxygen Transfer Coefficient in Bioreactors. Bioprocess Eng. 22(3) 2000: 261–265; https://doi.org/10.1007/s004490050730.

15 Linek V, et al. Gas–Liquid Mass Transfer Coefficient in Stirred Tanks Interpreted Through Models of Idealized Eddy Structure of Turbulence in the Bubble Vicinity. Chem. Eng. Process. Process Intensific. 43(12) 2004: 1511–1517; https://doi.org/10.1016/j.cep.2004.02.009.

16 Smith JM, van’t Riet K, Middleton JC. Scale-Up of Agitated Gas–Liquid Reactors for Mass Transfer. Proceedings of Second European Conference on Mixing. British Hydromechanics Research Association: Cambridge, UK, 1977: 51–66.

17 Zhu Y, Bandopadhayay PC, Wu J. Measurement of Gas–Liquid Mass Transfer in an Agitated Vessel: A Comparison Between Different Impellers. J. Chem. Eng. Jap. 34(5) 2001: 579–584; https://doi.org/10.1252/jcej.34.579.

18 Klöckner W, Büchs J. Advances in Shaking Technologies. Trends Biotechnol. 30(6) 2012: 307–314; https://doi.org/10.1016/j.tibtech.2012.03.001.

19 Klöckner W, et al. Correlation Between Mass Transfer Coefficient kLa and Relevant Operating Parameters in Cylindrical Disposable Shaken Bioreactors on a Bench-to-Pilot Scale. J. Biol. Eng. 7(1) 2013: 28; https://doi.org/10.1186/1754-1611-7-28.

20 Doig SD, et al. Modelling Surface Aeration Rates in Shaken Microtitre Plates Using Dimensionless Groups. Chem. Eng. Sci. 60(10) 2005: 2741–2750; https://doi.org/10.1016/j.ces.2004.12.025.

21 Henzler H-J, Schedel M. Suitability of the Shaking Flask for Oxygen Supply to Microbiological Cultures. Bioprocess Eng. 7, 1991: 123–131; https://doi.org/10.1007/BF00369423.

22 Nikakhtari H, Hill GA. Modelling Oxygen Transfer and Aerobic Growth in Shake Flasks and Well-Mixed Bioreactors. Can. J. Chem. Eng. 83(3) 2005: 493–499; https://doi.org/10.1002/cjce.5450830312.

23 Hermann R, Lehmann M, Büchs J. Characterization of Gas–Liquid Mass Transfer Phenomena in Microtiter Plates. Biotechnol. Bioeng. 81(2) 2003: 178–186; https://doi.org/10.1002/bit.10456.

24 Klöckner W, et al. Power Input Correlation To Characterize the Hydrodynamics of Cylindrical Orbitally Shaken Bioreactors. Biochem. Eng. J. 65, 2012: 63–69; https://doi.org/10.1016/j.bej.2012.04.007.

25 Zhu L, et al. Analysis of Volumetric Mass Transfer Coefficient (kLa) in Small- (250 mL) to Large-Scale (2500 L) Orbitally Shaken Bioreactors. 3 Biotech 10(9) 2020: 397; https://doi.org/10.1007/s13205-020-02352-9.

26 Nienow AW, Wisdom DJ, Middleton JC. Effect of Scale and Geometry on Flooding, Recirculation and Power in Gassed Stirred Vessels. Proceedings of the Second European Conference on Mixing. British Hydromechanics Research Association: Cambridge, UK, 1977.

27 Calderbank PH. Physical Rate Processes in Industrial Fermentation. Part I: The Interfacial Area in Gas–Liquid Contacting with Mechanical Agitation. Trans. Inst. Chem. Eng. 36, 1958: 443–463.

28 Chandrasekharan K, Calderbank PH. Further Observations on the Scale-Up of Aerated Mixing Vessels. Chem. Eng. Sci. 36(5) 1981: 819–823; https://doi.org/10.1016/0009-2509(81)85033-6.

29 Smith JM, Warmoeskerken MMCG. The Dispersion of Gases in Liquids with Turbines. Proceedings of Fifth European Conference on Mixing (Wurzburg, Germany, 1985). British Hydromechanics Research Association: Cambridge, UK, 1985; 115–126.

30 Linek V, Vacek V, Beneš P. A Critical Review and Experimental Verification of the Correct Use of the Dynamic Method for the Determination of Oxygen Transfer in Aerated Agitated Vessels to Water, Electrolyte Solutions and Viscous Liquids. Chem. Eng. J. 34(1) 1987: 11–34; https://doi.org/10.1016/0300-9467(87)85003-7.

31 Hickman AD. Gas–Liquid Oxygen Transfer and Scale-Up: A Novel Experimental Technique with Results for Mass Transfer in Aerated Agitated Vessels. Proceedings of Sixth European Conference on Mixing (Pavia, Italy, 1988). British Hydromechanics Research Association: Cambridge, UK, 1988; 369–374.

32 Smith JM. Simple Performance Correlations for Agitated Vessels. Proceedings of Seventh European Congress on Mixing (Brussels, Belgium, 1991). British Hydromechanics Research Association: Cambridge, UK, 1991; 233–241.

33 Whitton MJ, Nienow AW. Scale-Up Correlations for Gas Hold Up and Mass Transfer Coefficients in Stirred Tank Reactors. Proceedings of Third International Conference on Bioreactor and Bioprocess Fluid Dynamics (Cambridge, UK, 1993). British Hydromechanics Research Association: Cambridge, UK, 1993; 135–149.

34 Bakker A, van den Akker HEA. Gas–Liquid Contacting with Axial Flow Impellers. Trans. Inst. Chem. Eng. 72(A4) 1994: 573–582; https://www.bakker.org/cfm/publications/TransichemeGas1994.pdf.

A seasoned industry professional with a PhD in chemical and biological engineering from the University of British Columbia (Vancouver, Canada) and expertise in embryonic stem-cell bioengineering, upstream biological process development, and fed-batch bioreactors, Muhammad Arshad Chaudhry works as associate director of process and formulation development at Mural Oncology, 852 Winter Street, Waltham, MA 02451; [email protected].