Measuring kLa for Better Bioreactor Performance

Knowledge of k_La (the volumetric mass-transfer coefficient that describes the efficiency with which oxygen can be delivered to a bioreactor for a given set of operating conditions) is not new. Here I provide information for those who are unfamiliar with the measurement method and/or issues that must be considered when making these measurements. Advances in this area now make it advisable to run k_La measurements routinely in many bioprocesses.

The Importance of Measuring k_La

Before examining the process theory and tactical specifics of k_La determinations, it is essential to understand why k_La measurements are relevant and how they add value to bioprocesses. Dissolved oxygen (DO) is often the limiting substrate in fermentation and cell-culture systems. For bacteria and yeast cultures, the critical oxygen concentration is usually 10–50% of air saturation. Above that critical level, the oxygen concentration no longer limits growth. For optimum growth, it is therefore important to maintain DO levels above the critical value by sparging (bubbling gas through) the bioreactor with air or pure oxygen. Of course, to be effective, the mass transfer rate of oxygen to the liquid broth must equal or exceed the rate at which growing cells take up that oxygen.

PRODUCT FOCUS: ALL BIOPHARMACEUTICALS

PROCESS FOCUS: PRODUCTION

WHO SHOULD READ: PROCESS AND PRODUCT DEVELOPMENT

KEYWORDS: CELL CULTURE, BIOREACTOR, OXYGEN ANALYSIS,k_la

LEVEL: INTRODUCTION

Measurements of k_La provide important information about a bioprocess or bioreactor. These determinations ensure that processing conditions are such that an adequate supply of oxygen is available for proliferation of cells. The k_La value can also be used to optimize control variables over the lifecycle of a bioprocess. Such optimization would be based on the oxygen demand at various points in the process and growth phase of the biological. Criteria for optimization may be product yield, power consumption, or processing time.

Applications

New equipment: Measurements of k_La are made when evaluating new reactor designs, new gas sparging equipment, and/or operating conditions. The goal in each case is to confirm that reactor conditions can support a system being processed at each point in its lifecycle.

Process Optimization: Measuring k_La is also critical during process optimization. In scale-up and manufacturing situations, fine-tuning bioreactor performance assumes greater significance. Measuring k_La is key to controlling oxygenation at the optimal rate (1).

Relevance to Single-Use Bioreactors: Determining k_La can be especially useful when companies make decisions about the role of single-use bioreactors in their overall manufacturing strategy. For those considering adopting single-use bioreactor technology and thinking about where and how to do so, k_La measurements can provide meaningful support for big investment decisions. The range of k_La values that a SUB can support, coupled with the operating conditions required to achieve that range, are fundamental in the selection of reactor equipment. A review of the process involved explains why.

Process Theory

The oxygen transfer rate (OTR) of a bioreactor is strongly influenced by the hydrodynamic conditions being used in the bioprocess it’s used in (Figure 1). These conditions are a function of energy dissipation that depends on the operating conditions, the physicochemical properties of a culture, the geometrical parameters of the bioreactor, and the presence of oxygen-consuming cells.

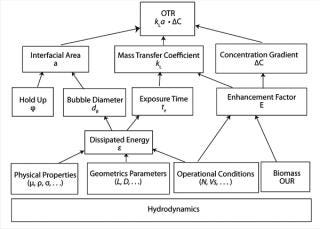
Figure 1: ()

During cell culture, oxygen is transferred from a gas (typically a bubble or headspace) to a liquid, so it can ultimately be absorbed into a cell and consumed. In the simplest terms, this process can be described as the flux across a barrier layer expressed as the product of the driving force (mass imbalance) and mass transfer coefficient (k_La) in Equation 1 below:

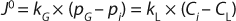
In that equation, J⁰ is the molar flux of oxygen (mol/m²s) through the gas–liquid interface, k_G and k_L are the local mass transfer coefficients, p_G is the oxygen partial pressure in the gas phase, and C_L is the dissolved oxygen concentration in the liquid. Index i refers to values at the gas–liquid interface.

Because interfacial concentrations are not directly measureable, it is common to consider a special case of Equation 1 that describes flux under or at equilibrium:

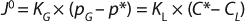
In Equation 2 above, p* is the oxygen pressure in equilibrium with the liquid phase, C* is the oxygen saturation in the bulk liquid, and K_G and k_L are the overall mass transfer coefficients. However, because the solubility of oxygen in water is very low and the vast majority of mass-transfer resistance is on the liquid side of the interface, the overall mass transfer coefficient can be assumed to be equal to the local coefficient (K_L = k_L). As a result, the oxygen mass transfer rate per unit of reactor volume (dCO₂/dt) is obtained by multiplying the overall flux by the gas–liquid interfacial area per unit liquid volume using Equation 3

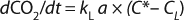
Quantification and Equations Used

The mass balance for the DO in the well-mixed liquid phase is described in Equation 4

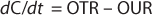
Here, dC/dt is the accumulation oxygen rate in the liquid phase, OTR represents the oxygen transfer rate from the gas to the liquid, and OUR is the oxygen uptake rate by the microorganisms. The last term can be expressed by the product qO₂ × CX, with qO₂ being the specific oxygen uptake rate of the microorganism used and CX is the biomass concentration.

In the absence of biomass or with nonrespiring cells, when biochemical reactions do not take place, OUR = 0. In this case, Equation 4 can be simplified as

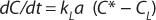
Because of the difficulty of measuring k_L and a separately, the product k_La is treated as a single measureable variable: the volumetric mass transfer coefficient. Determination of k_La is achieved by recording the system response following a perturbation of the equilibrium oxygen concentration.

Integrating the expression of previous equation yields Equation 5

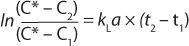
Here, C_i is the concentration of oxygen at time t_i. For the case of a system perturbation that increases the DO concentration from an initial value of 0, this equation becomes

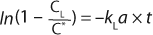
For the case of a perturbation that decreases the dissolved oxygen concentration, the equation becomes

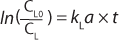
Factors Affecting k_La

Multiple Variables: As illustrated in Figure 1, k_La is influenced by many variables. Factors include everything from a bioreactor’s size and design to the sparging of gas, mixing, cell line, media type, temperature, pH, salt content, and antifoaming agents (2). Every time one of those factors changes, the dynamics of the bioprocess, including k_La, change as well. Given such broad vulnerability, it is not surprising that actual in-process k_La measurement has been limited. Scientists have relied to a large extent on the built-in functionality of the bioprocesser to maintain proper oxygen flow rate.

Speed: Because k_La measurements involve monitoring levels of DO following a system perturbation, the results can be influenced by the response time (or “speed”) of a sensor making those determinations. Sensors with response times (τ_r) on the order of the first-order time constant of the mass transfer (1/ k_La) require special treatment of their data to correct for the time lag in readings introduced by the oxygen sensor.

A general rule of thumb is that the sensor response time must be less than one tenth of the time constant for mass transfer for this effect to be negligible (3,4). When a sensors response time does not meet this requirement, the data must be treated with Equation 6

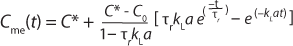
in which C_me(t) is the measured value of oxygen at time t. That equation cannot be linearized, so nonlinear fitting of observed response data is required to derive the value of k_La.

Changes in Reactor Vessel Size: The value of k_La is unique to both the size and configuration of a reactor vessel. Although some empirically derived expressions have been published for predicting k_La values in non-Newtonian fluids, there is no agreed upon set of equations that account for all of the variables that can affect the results. Accordingly, predicting k_La is not possible, and k_La studies need to be performed for bioreactors individually.

Measuring k_La

The value of k_La rate constants can be ascertained for virtually any reactor vessel, from a shaker flask to the most sophisticated single-use bioreactor. It is important to recognize that, as noted above, the sensitivity of k_La to many different factors also results in changes in the best way to measure it. Similarly, the differences in disposable bioreactor construction and operating methodology often indicate the need to modify the general instructions for k_La measurement. This is not necessarily difficult, but rather is simply a reflection of differences in bioreactors.

Benefits

Measuring k_La offers important benefits:

For companies engaged in bioprocessing, the ability to measure k_La easily and accurately represents a significant opportunity to improve the performance of their operations.

About the Author

Author Details
James Kane, PhD, is vice president of technology and product development at Polestar Technologies, Inc; 220 Reservoir Street #3, Needham Heights, MA, USA 02494; 1-781-449-2284; www.polestartech.com.

REFERENCES

1.) Arrua, LA, BJ McCoy, and JM. Smith. 1990. Gas–Liquid Mass Trans
fer in Stirrer Tanks. AlChE J 36:1768-1772.

2.) Lydersen, BK, NA D’Elia, and KL Nelson.

3.) Weiland, P, and U. Onken. 1981. Fluid Dynamics and Mass Transfer in Airlift Fermentor with External Loop. Ger. Chem. Eng. 4:42-50.

4.) Godbole, SP. 1984. Hydrodynamics and Mass Transfer in Non-Newtonian Solutions in a Bubble Column. AlChE J. 30:213-220.